¶ 開発環境の確認
¶ 開発環境
このチュートリアルでは、以下の開発環境を想定します。
- Anaconda 2.5.3
- Python 3.11.10
- Visual Studio Code 1.95.0
¶ 使用するライブラリー
使用するライブラリーは以下のものです。
- numpy
- matplotlib
- random
- pulp
- networkx
- osmnx
PuLPは線形計画問題用のライブラリー、NetworkXはグラフやネットワーク理論の計算用のライブラリー、そして、OSMNXはOpenStreetMapというオープンソースの地図データを活用するためのライブラリーです。
Anacondaに仮想環境を作成し、これらのライブラリーをインストールしておきます。
¶ 演習内容
このチュートリアルでは以下の演習を行います。
- OSMNXを使って地図情報を取得する
- OSMNXとNetworkXを使って最短経路を取得する
- PuLPを使って取得した地点の巡回路を取得する
¶ OSMNXを使って地図情報を取得する
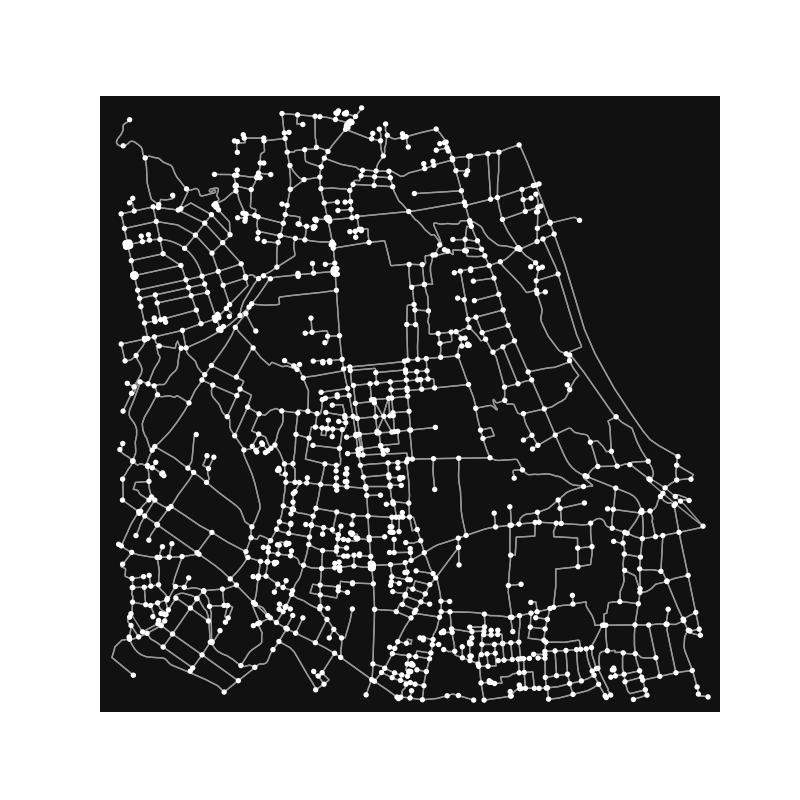
¶ 施設名からの地図の取得
次に、施設名称からの地図の取得方法を説明します。ここでは、神奈川工科大の周りの地図を取得します。OpenStreetMapでは地図情報をノードとエッジに分けて管理しているのですが、やり方としては、神奈川工科大学の最寄りのノードを取得し、そのノードを中心とした地図（ここでは1000m四方）を取得します。
import numpy as np
from matplotlib import pyplot as plt
import osmnx as ox
import networkx as nx
import random
import pulp
# 施設名
# 緯度経度
lat, lon = ox.geocoder.geocode("神奈川工科大学")
G=ox.graph_from_point((lat,lon), dist=1000)
ox.plot_graph(G)
実行結果は以下のようになります。
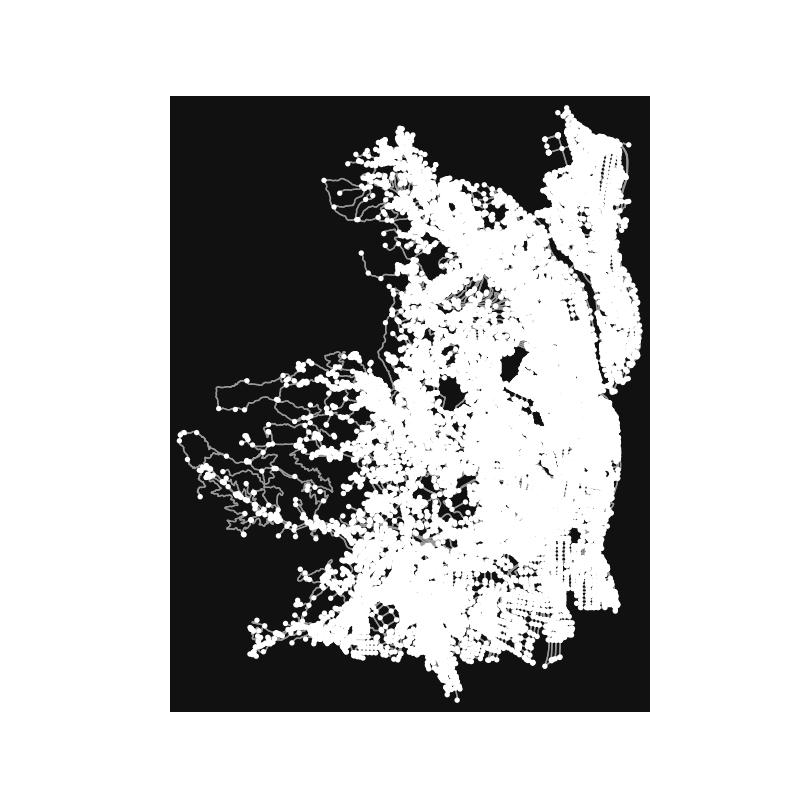
¶ 市区町村名を使った地図の取得
OSMNxでは市区町村名を使って地図情報を取得することができます。以下に神奈川県厚木市の地図情報を取得し、描画するコードを紹介します。
import numpy as np
from matplotlib import pyplot as plt
import osmnx as ox
import networkx as nx
import random
import pulp
# 市区町村名
city = "Atsugi, Kanagawa, Japan"
# 地図情報の取得と描画
G = ox.graph_from_place(city)
ox.plot_graph(G)
実行結果は以下のようになります。
この場合、以下のようにすると複数の市町村の地図を取得することもできます。
import numpy as np
from matplotlib import pyplot as plt
import osmnx as ox
import networkx as nx
import random
import pulp
# 市区町村名
city1 = "Atsugi, Kanagawa, Japan"
city2 = "Isehara, Kanagawa, Japan"
# 地図情報の取得と描画
G1 = ox.graph_from_place(city1)
G2 = ox.graph_from_place(city2)
G = nx.compose_all([G1, G2])
ox.plot_graph(G)
実行結果は以下のようになります。
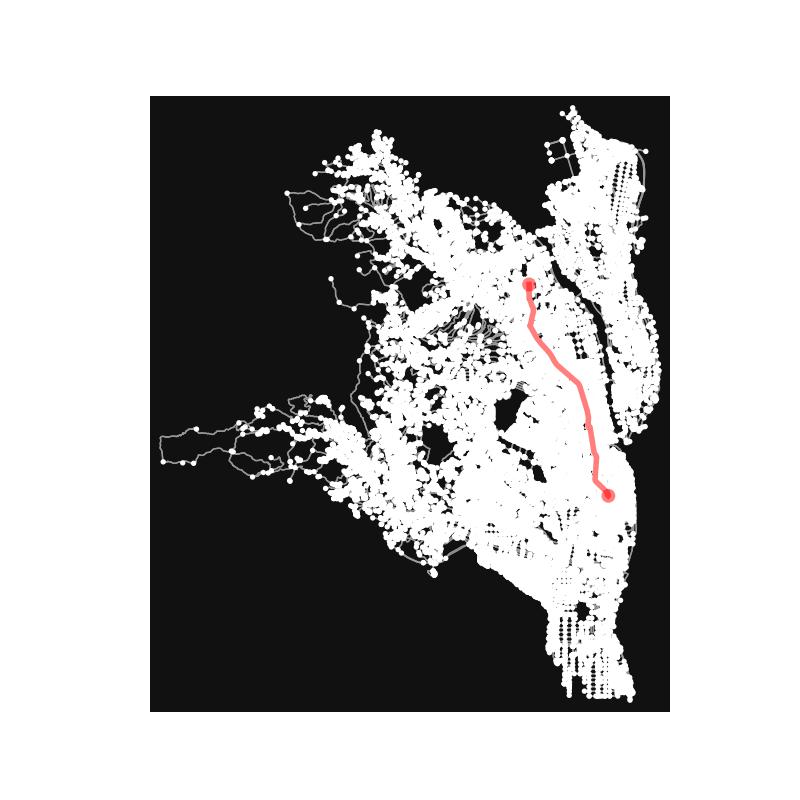
¶ OSMNXとNetworkXを使って最短経路を取得する
それでは次に、2点間の最短経路を取得し、経路長を求めてみます。ここでは、神奈川工科大学と本厚木駅間を例に試してみます。
import numpy as np
from matplotlib import pyplot as plt
import osmnx as ox
import networkx as nx
import random
import pulp
# 市町村名
city = "Atsugi, Kanagawa, Japan"
# 地図情報の取得
G = ox.graph_from_place(city)
# 始点と終点を取得
slat, slon = ox.geocoder.geocode("神奈川工科大学")
sid=ox.distance.nearest_nodes(G, slon, slat)
dlat, dlon = ox.geocoder.geocode("本厚木駅")
did=ox.distance.nearest_nodes(G, dlon, dlat)
# 最短経路情報を取得
d = nx.shortest_path_length(G, source=sid, target=did, weight='length')
print(f"距離：{d}メートル")
# 地図の描画
route = nx.shortest_path(G, sid, did, 'length')
ox.plot_graph_route(G, route)
NetworkXの関数（shortest_path_length、shortest_path）を使用することで、距離の取得と最短経路の取得ができることが分かります。
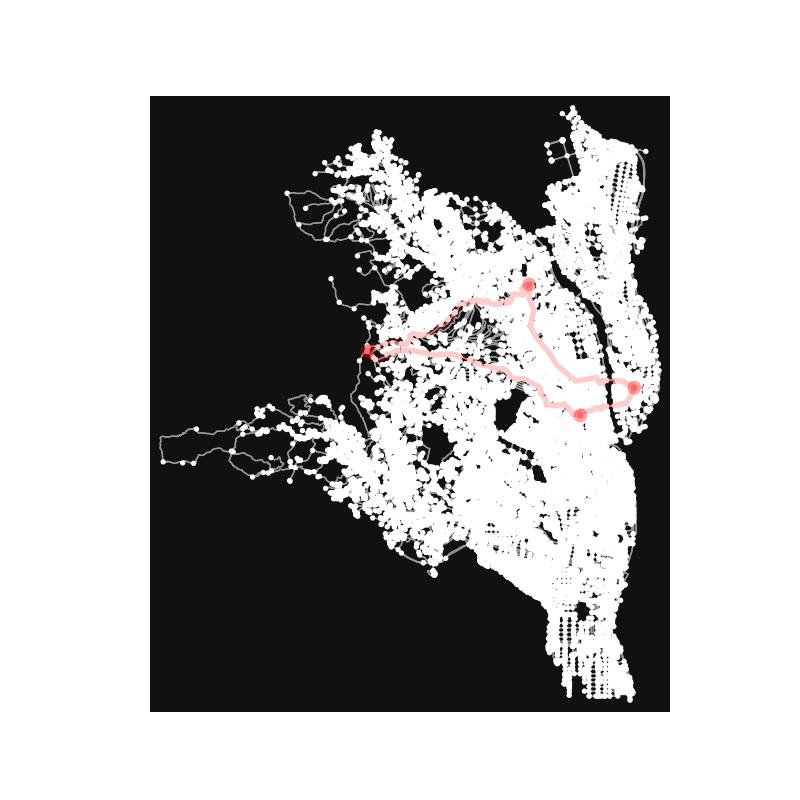
¶ PuLPを使って取得した地点の巡回路を取得する
次にいよいよ巡回路の取得を目指します。この巡回路の取得は、いわゆる「巡回セールスマン問題」と呼ばれているもので、最適解を求めるのが困難な問題として知られています。n拠点を対象に考えると、考えられるルート数はn!となります。nが大きくなるとその計算量が膨大になることは想像できると思います。このように計算量が大きくなりますが、実用的な問題であるため、多くのヒューリスティック解が提案されています。
このチュートリアルでは、そのような大規模な問題を取り扱わず、数拠点を巡回する問題を取り扱うため、線形問題として立式し、数理計画問題を解くためのライブラリーであるPuLPを用いて、最適解の取得を目指します。
式(1)は目的関数です。地点間の距離に、バイナリ変数であるをかけることで、移動距離を計算することができます。
式(2)は各拠点の出発の制約です。すべての目的候補地に対して、合計が1であるということで制約を実現しています。逆に式(3)は、すべての出発候補地からの合計が1であるということで、到着地の制約を表現しています。式(4)はすべての経路を通らないルートを除去するための制約です。簡単な例では、4拠点があった場合、(2)(3)の制約のみでは、というルートも可能となってしまうということです。このようなルートは、サブツアーと呼ばれるようです。そのようになr内容にするために制約(4)が必要となります。
では、ここでは、神奈川工科大を出発し、厚木市内の任意の拠点3か所を回って、再び神奈川工科大に戻ってくるという問題を解いてみます。
import numpy as np
from matplotlib import pyplot as plt
import osmnx as ox
import networkx as nx
import random
import pulp
# 市町村名
city = "Atsugi, Kanagawa, Japan"
# 地図情報の取得
G = ox.graph_from_place(city)
# 始点を取得
slat, slon = ox.geocoder.geocode("神奈川工科大学")
sid=ox.distance.nearest_nodes(G, slon, slat)
# 訪問拠点数
num_nodes = 3 + 1 # +1は神奈川工科大分
# ランダムにnum_nodesか所のIDを取得
ids = [random.randint(0, len(G)-1) for p in range(0, num_nodes-1)]
print(ids)
node_list = []
node_list.append(sid) #最初は神奈川工科大学
for key in ids:
node_list.append((list(G.nodes(data=True))[key])[0])
## 距離計算関数の定義
# 2つのノード間の最短経路の長さ（移動時間）を計算する関数
def dist(sid,did):
try:
d = nx.shortest_path_length(G, source=sid, target=did, method='dijkstra', weight='length')
except:
d = np.nan
return d
## 関数の適用
# 巡回対象の各ノード間で関数 dist を適用し、距離行列を計算
distance_matrix = np.asarray([[dist(k,l) for l in node_list] for k in node_list])
print(distance_matrix)
# モデルの作成
prob = pulp.LpProblem("Travelling Salesman Problem", pulp.LpMinimize)
# 決定変数の定義
x = pulp.LpVariable.dicts(
"route",
((i, j) for i in range(num_nodes) for j in range(num_nodes) if i != j),
cat='Binary')
# 目的関数
prob += pulp.lpSum(
x[i, j] * distance_matrix[i, j] for i in range(num_nodes) for j in range(num_nodes) if i != j
)
# 制約条件
for i in range(num_nodes):
prob += pulp.lpSum(x[i, j] for j in range(num_nodes) if i != j) == 1 # 制約式(2)
prob += pulp.lpSum(x[j, i] for j in range(num_nodes) if i != j) == 1 # 制約式(3)
# サブツアー除去制約
u = pulp.LpVariable.dicts("u", range(1, num_nodes), lowBound=0, upBound=num_nodes-1)
for i in range(1, num_nodes):
for j in range(1, num_nodes):
if i != j:
prob += u[i] - u[j] + (num_nodes-1) * x[i, j] <= num_nodes -1 - 1
# 最適化計算
prob.solve(pulp.PULP_CBC_CMD(msg=1))
# 結果の表示
print(f"総移動距離: {pulp.value(prob.objective):.2f}")
# 最適ルートの取得
route = [0] # 配列のIDを使った最適ルート
while len(route) < num_nodes + 1:
added = False
for j in range(num_nodes):
if j not in route and pulp.value(x[route[-1], j]) == 1:
route.append(j)
added = True
break
if not added:
break
# マップ上のIDを使った最適ルートに変換
route_id_list = [node_list[i] for i in route]
print("最適ルートID:", route_id_list)
# 構成するルートの取得
route_list = []
for k in range(num_nodes):
fm = k
if k == num_nodes-1:
to = 0
else:
to = k + 1
shortest_route = nx.shortest_path(G, route_id_list[fm], route_id_list[to], 'length')
route_list.append(shortest_route)
# ルートの描画
ox.plot_graph_routes(G, route_list, route_alpha=0.2)
コードは少し長いですが、コメントとPuLPの使い方を紹介した記事などを見ながら読めば、どのようなことをやっているのかはおおむね理解できると思います。最適化エンジンとしては、CBCというものを使用しましたが、他にも無償で利用できるものもありますので、いろいろ試してみてください。CBCのオプションとして、msgのみ書きましたが、msg=1とすると、計算時間なども表示されますので、他のオプションも含め、是非試してみてください。
